|
For a review of point reflections, see the Refresher section Transformations: Reflections.
Now let's expand that knowledge of reflections in relation to geometry.
 |
A reflection in a point P is a transformation of the plane such that the image of the "fixed" point P is P, and for all other points, the image of A is A' where P is the midpoint of 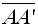 . |
|
A point reflection exists when a figure is built around a single point
called the center of the figure, or point of reflection.
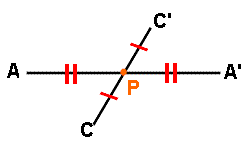
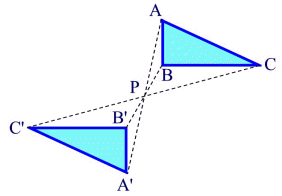
The diagram above shows points A and C reflected through point P.
Notice that P is the midpoint of segments
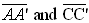 . . |
For every point in the figure, there is another point found directly opposite it on the other side of the center such that the point of reflection becomes the midpoint of the segment joining the point with its image.
Point reflection may also be referred to
as point symmetry.
|

 Easily recognized: A point reflection in the plane can be easily recognized because the resulting image will be the same as if it had been rotated 180 degrees about the given center point. Easily recognized: A point reflection in the plane can be easily recognized because the resulting image will be the same as if it had been rotated 180 degrees about the given center point.
In this manner, a point reflection can also be called a half-turn
(or a rotation of 180º).
If the point of reflection is P, the notation may be expressed
as a rotation, 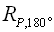 . . |
|
 |

|
 |
A point reflection creates a figure that is congruent to the original figure and is a rigid transformation (isometry).
Notations:
(reflection notation): rorigin
(rotation notation): 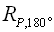 |
Properties preserved under a
point reflection from pre-image to image.
1. distance (lengths of segments remain the same)
2. angle measures (remain the same)
3. parallelism (parallel lines remain parallel)
4. collinearity (points remain on the same lines)
5. midpoint (midpoint remain the same in each figure.)
6. orientation (lettering order remains the same)
|
|
Since the orientation in a point reflection remains the same
(such as counterclockwise
seen in this diagram above),
a point reflection is more specifically called a direct rigid transformation (or isometry).
|
Since the orientation in a point reflection remains the same
(such as counterclockwise seen in this diagram),
a point reflection is more specifically called a direct rigid transformation.


Point Reflection in the Coordinate Plane:
While any point in the coordinate plane may be used as a point of reflection,
the most commonly used point is the origin.
Under a point reflection in the origin the image of (x, y) is (-x, -y).
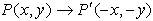 or or 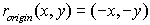
|
|
Point reflection in the origin:
(x, y) → (-x, -y)
(this is also the mapping for a rotation in the origin of 180º)
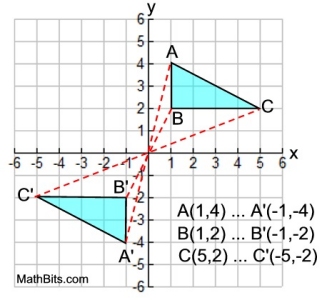 |
Point Reflection in Origin
Triangle A'B'C' is the image of triangle ABC after a point reflection in the origin.
Imagine a straight line segment connecting A to A' where the origin is the midpoint of the segment.
Also, the origin is the midpoint of the segments connecting B to B ',
and C to C '.
|
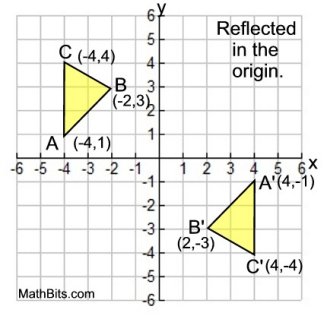
|
Point Reflection in Origin
Notice how the coordinates of triangle A'B'C' are the same numeral value as triangle ABC, BUT the signs have been changed.
(x, y) → (-x, -y)
Triangle ABC has been reflected in the origin.
|
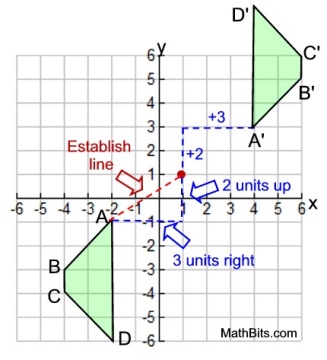
|
Point Reflection in (1,1)
If a point reflection is NOT centered
in the origin, you CANNOT use the map
(x, y) → (-x, -y).
But you can find the coordinates of the image:
• connect one pre-image vertex to (1,1)
Now you have the "line" that will connect to the coordinating image vertex.
Remember (1,1) will be the line segment midpoint.
• use "rise" and "run" to move
to the new image vertex.
• repeat for all vertices, and
you have the image.
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|


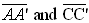 .
.